GAMES202 - Real-time shadows


    
  1. 1. 1 Shadow Mapping
  2. 2. 2 Shadow Mapping的数学原理
  3. 3. 3 软阴影 —— Percentage closer soft shadows(PCSS)
    1. 3.1. 3.1 Percentage Closer Filtering(PCF)
    2. 3.2. 3.2 Percentage Closer Soft Shadows(PCSS)
  4. 4. 4 Variance Soft Shadow Mapping(VSSM)
    1. 4.1. 4.1 降低 PCF 开销
    2. 4.2. 4.2 降低 blocker search 的开销
    3. 4.3. 4.3 MIPMAP 和 Summed-Area Variance Shadow Map
  5. 5. 5 Moment Shadow Mapping
  6. 6. 6 Distance Field Soft Shadows
    1. 6.1. 6.1 SDF
    2. 6.2. 6.2 Distance Field Soft Shadows

1 Shadow Mapping

  • 渲染两趟(2-pass)
  • 是一个图像空间中的算法
  • Pass 1
    • 从光源位置渲染场景，输出离光源最近的深度，即为shadow map
  • Pass 2
    • 从相机出发，先找到当前像素位置看到的物体表面位置
    • 从该位置向光源方向投影到shadow map上，查找是否被遮挡
  • 相较于shadow ray的优势
    • shadow ray在每个交点处对所有光源发射，每发射一次都要与场景求交，开销大
    • shadow map只需要在第一趟求交，之后判断遮挡只需要查询shadow map
  • 优点
    • 不需要了解场景的实际几何分布，只需要有shadow map
  • 缺点
    • shadow map将场景的深度分布离散化，在一个像素区域内深度值为常数
    • 容易造成自遮挡、锯齿
  • 自遮挡解决办法
    • 增加小量bias，只有距离超过bias才认为被遮挡
    • bias可以为变量，例如根据夹角动态地调整
    • 如果bias过大，会造成不接触的阴影(detached)
  • Second-depth shadow mapping
    • 在shadow map中储存第二小的深度
    • 将最小深度和第二小深度的中间值作为深度比较的参考值
    • 解决自遮挡问题，并且不需要引入bias
    • 缺点
      • 模型必须封闭(watertight)
      • 维护两个最小值，开销更大

2 Shadow Mapping的数学原理

  • 实时渲染中，许多不等式都把它看做左右两边近似相等

  • 重要近似：

    img

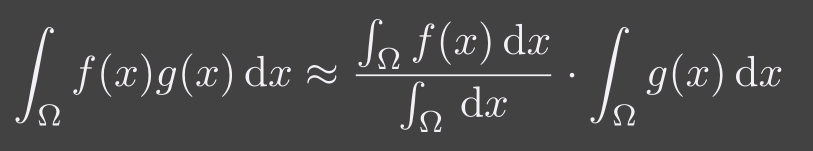
    • 分母用于将f(x)的积分值归一化

  • 什么时候该近似比较准确

    • 积分区域比较小
    • g(x)在积分域范围内变化非常小(smooth)

  • 利用该近似处理渲染方程

    img

    • 把visibility项提出来
    • 左边是visibility，右边是shading
    • 即为shadow map的思路
    • 为何shadow mapping的近似是准确的
      • 光源为点光源/方向光源时，只需要在一个点/一个方向上积分，积分域很小
      • 光源亮度为常数、brdf为diffuse时，右边shading项的值是smooth的

3 软阴影 —— Percentage closer soft shadows(PCSS)

3.1 Percentage Closer Filtering(PCF)

  • 用于做抗锯齿(anti-aliasing)

  • filter不是对最后的生成结果做，也不是对shadow map做，而是在阴影判断的时候做

  • 算法思路

    • 之前的visibility值是非0即1的，而该算法中visibility是一个0到1之间的值
    • 在shadow map中查询时，改为查询目标位置附近的一个block，并对查询结果做平均

  • 例子

    img

  • filter越小，阴影越硬；filter越大，阴影越软

    • 由此思路，可以利用PCF算法做软阴影效果

3.2 Percentage Closer Soft Shadows(PCSS)

  • 软阴影的形成原因：现实中的光源一般不是点光源，而是有一点宽度的光源

  • 观察现实中的阴影发现，影子距离遮挡物越远，表现的效果越软

  • 示意图

    img

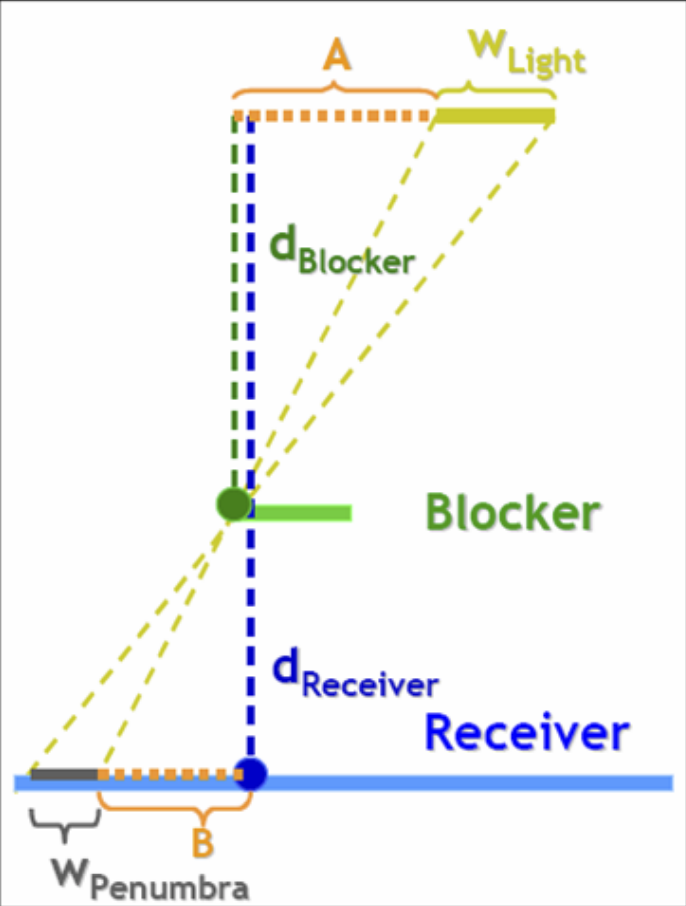
  • $w{Penumbra}$越大，阴影越软；其大小与光源宽度$w{light}$以及blocker在光源与receiver之间的位置有关

  • 由相似三角形关系可得：

    img

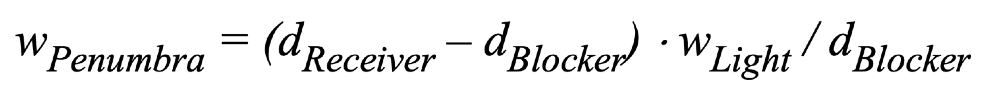
  • 算法流程

    1. 在面光源处生成一张shadow map
      • 把面光源看做在其中心位置的一个点光源，以生成shadow map
    2. 找到blocker对应的所有像素 (blocker search)
      • 对于一个shading point，在shadow map中取对应的一个区域，判断遮挡关系
      • 对这些遮挡位置的深度值做平均，记为blocker的深度
      • 注意是对遮挡物的深度做平均，而不是对整个区域做平均！
    3. 确定filter大小
      • 根据平均得到的blocker深度，根据上面的数学公式，确定filter的size
    4. 执行PCF操作

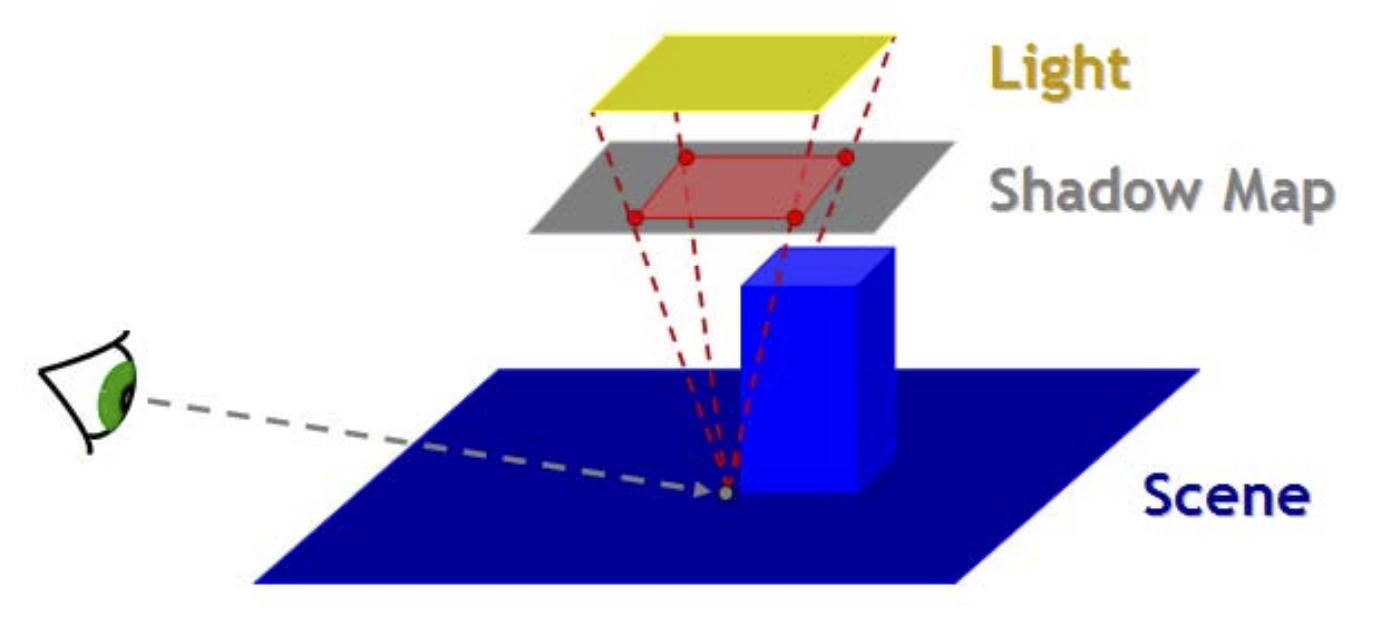
  • 如何确定第2步中搜索shadow map的范围

    • 可以根据到面光源的视锥与shadow map的相交区域确定

      img

符号函数 $\chi^+(x) = x > 0 ? 1 : 0$

  • 开销主要在第2步和第4步中
    • 在区域中查询每一个像素需要花费大量时间
    • 阴影越软，需要越大的filter区域，运行时间更长
  • 优化思路：不查询整个区域，而是对区域进行部分采样
    • 缺点：产生的结果有噪声
    • 然而，现代技术对噪声的容忍度不断提升，因为后续可以在图像空间对结果进行降噪
    • 因此现在一般都是在用PCSS

4 Variance Soft Shadow Mapping(VSSM)

  • 针对性的解决 PCSS 中开销大的步骤
  • 令 t 为 shading point 处的深度值

4.1 降低 PCF 开销

  • 本质问题 —— 判断区域内有多少比例的 texel 比当前 shading point 的距离 t 要近
  • 思路：快速地计算区域内深度值的均值和方差，并用正态分布去拟合，从而得到近似的比例值
  • 求均值
    • 硬件MIPMAP
    • Summed Area Tables (SAT)
  • 求方差
    • $Var(X) = E(X^2) - E^2(X)$
    • 可以在shadow map中额外增加一个通道，用于存储 $X^2$ 的值
  • 引入切比雪夫不等式
    • $P(x>t) \le \frac{\sigma^2}{\sigma^2 + (t - \mu)^2}$，前提：t 必须在 $\mu$ 的右边
    • 甚至不需要假设它的分布为正态分布！
    • 实时渲染中，不等号看做约等号
  • 性能分析
    • shadow map 生成
      • 在生成 shadow map 的同时，再同时生成一张 square depth map
    • 运行时间
      • 范围内深度均值：O(1)
      • 范围内深度平方的均值：O(1)
      • 切比雪夫：O(1)
      • 不需要采样和循环遍历

4.2 降低 blocker search 的开销

  • 我们需要得到遮挡物的平均深度，记作 $z{occ}$，未遮挡的平均深度记作 $z{unocc}$
  • 观察可知： $\frac{N1}{N} z{unocc} + \frac{N2}{N} z{occ} = z_{avg}$
  • 近似结果：
    • N1 / N = P(x > t) → 由切比雪夫不等式解决！
    • N2 / N = 1 - P(x > t)
    • 未遮挡的深度全部认为和 shading point 的深度一样，即 $z_{unocc} = t$

4.3 MIPMAP 和 Summed-Area Variance Shadow Map

  • 快速得到矩形区域范围内的均值
  • Mipmap
    • 快速、近似、矩形
    • 是个近似结果，有些情况需要三线性插值
  • Summed-Area Table (SAT)
    • 二维前缀和
    • 准确值
    • 会引入一些额外开销
      • 构建时需要 O(n) 的时间复杂度以及 O(n) 的空间复杂度

5 Moment Shadow Mapping

  • VSSM的缺陷

    • 在某些情况下近似的结果不准
      • 偏黑 - 通常能忍受，偏白 - 漏光！
    • 切比雪夫不等式只在 $t > z_{avg}$ 的时候准确

  • 目标：让深度的分布更准确

  • 思路：使用更高阶的矩 (Moment) 来描述分布

  • 矩 (Momenet)

    • 最简单的形式： $x, x^2, x^3, x^4, \cdots$
    • VSSM使用了前两阶的矩

  • 用前 m 阶矩描述分布的累积分布函数(CDF)

    • 类似于某种展开

    • 展开的越多，越接近PCF得到的准确值

      img

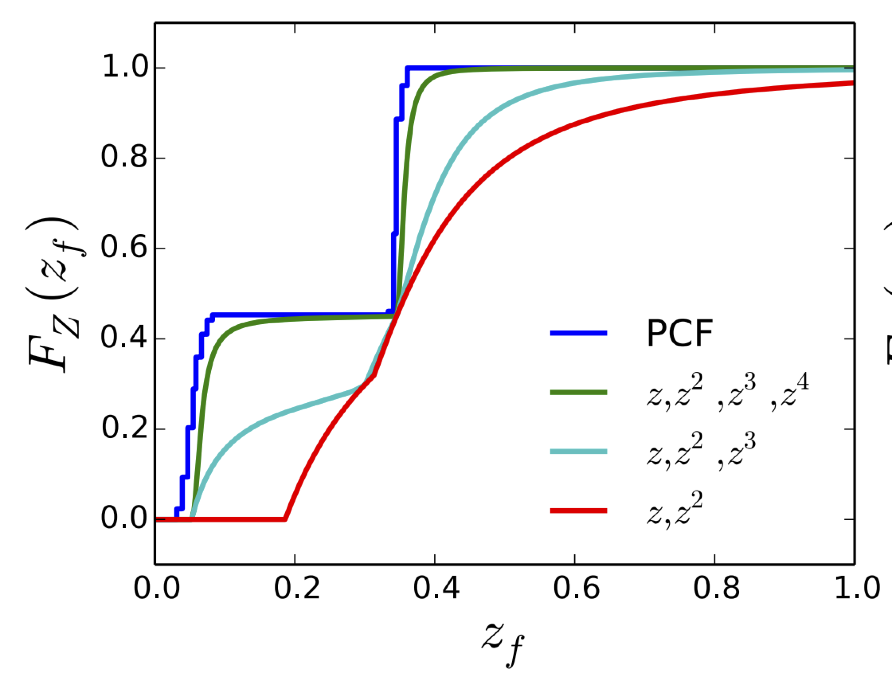
    • 一般取 4 ，得到一个更准确的近似结果

    • 表达式非常复杂

  • 缺点

    • 存储量增加
    • 运算消耗增加

6 Distance Field Soft Shadows

6.1 SDF

  • SDF = Signed Distance Field，有向距离场

  • Distance function

    • 定义空间中的任何一点到给定物体表面的最小距离
    • 距离可以带正负号

  • 如何计算 Distance function

    • 使用空间划分的结构
      • 八叉树等

  • 前沿拓展：optimal transport

  • 应用

    • 使用Ray marching / Sphere tracing 来计算光线与 SDF 的交点

      img

      • 任意一点的 SDF 值定义了该点处的一个安全距离
      • 在这个安全距离范围内，一定不会与任何物体相交
      • 从光线起点开始，每次前进 SDF(p) 的距离，直到找到交点

    • 使用SDF生成软阴影

      img

      • 可以用 SDF 来得到被遮挡比例的近似值
      • 根据 SDF 给出的安全距离，得到一个对应的安全角度
      • 在这个安全角度内，没有任何遮挡物
      • 如果安全角度越小，那么 visibility 越小

    • 字体渲染

      • 可以得到任意分辨率下的高清字体

6.2 Distance Field Soft Shadows

  • 用安全角度的大小来近似 visibility 值，从而得到不同亮度的阴影 → 软阴影

  • 计算安全角度

    img

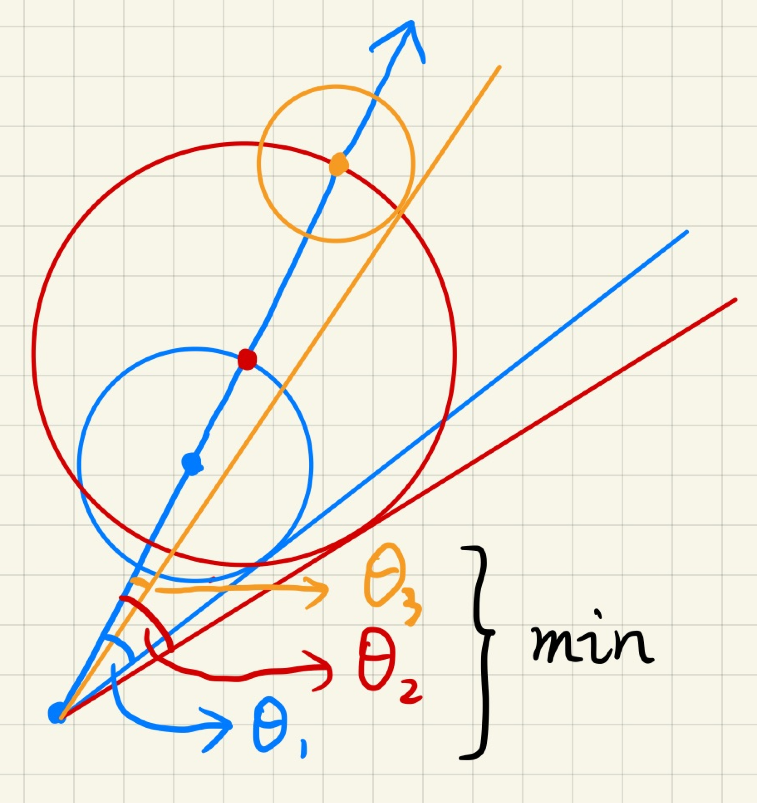
    • 在 ray marching 的过程中，每一步都计算当前的安全角度值
    • 取所有角度的最小值，作为最终结果
    • 如何得到角度
      • 准确值： $\arcsin \frac{SDF(p)}{p - o}$
      • 近似值： $\min { \frac{k \cdot SDF(P)}{p - o} , 1.0}$
        • k 越大，近似值越容易取到 1，阴影越硬
        • k 可以控制阴影的软硬程度

  • 优点

    • 快
      • 在ray marching的过程中，与生成硬阴影的速度相当
    • 高质量

  • 缺点

    • 需要预计算
    • 需要大量的存储空间
    • 无法使用在变形物体上

扫一扫，分享到微信

微信分享二维码

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true